Introducción

Una de las maneras de identificar comportamientos tipo criticalidad autoorganizada o self-organized criticality (SOC) es identificando leyes de potencia (PL) o escala en el fenómeno que estemos estudiando. La distribución normal o gaussiana y las PL responden a dos maneras muy distintas de ver el mundo. Ambas visiones difieren radicalmente. Sin embargo, se han realizado grandes esfuerzos para que las distribuciones clásicas abarquen muchos fenómenos sociales, económicos, biológicos y acontecimientos extremos o deportivos, utilizando para ello los modelos lineales estándares de la regresión múltiple, en un esfuerzo hasta ahora inútil de explicar tales acontecimientos1. Ahora bien, si asumimos que hay dependencia entre los factores que afectan a un determinado fenómeno, lo natural es que emerjan distribuciones que siguen PL2,3.

Los sistemas más importantes que encontramos en la naturaleza (tanto geológicos; como biológicos; ecológicos; climáticos, etc.), así como los aspectos vinculados al deporte y sus practicantes, tienen una estructura jerárquica, es decir se configuran en estratos o niveles distintos a los que corresponden escalas características de tiempo, longitud o energía. Aunque las leyes básicas de la naturaleza no cambian sea cual sea la escala a la que los estudiamos, sí cambia la fenomenología que presentan. De hecho, explicar o intentar relacionar los fenómenos o el comportamiento de estratos de niveles más altos con los inferiores presenta múltiples problemas. Es entonces cuando la aplicación de PL adquiere un papel relevante en el estudio del deporte y lo que justifica su aplicación para ejemplificar su existencia en el entrenamiento y/o la propia actividad deportiva4.

El objetivo de este trabajo es analizar cómo pueden ser utilizadas las PL en el deporte y comprobar si la información que proporcionan puede ser de utilidad para incrementar la calidad y cantidad de información de la que pueden disponer los técnicos deportivos en el desempeño de su actividad profesional.

Leyes de potencia, alometría y deporte

Es sabido que el perfil del deportista cambia con la modalidad deportiva. Esto afecta a todos los aspectos o planos que influyen en el rendimiento (inteligencia, control motor, actitudes, capacidades, etc.) y, por lo tanto, también en su morfología1. Así, para triunfar en el culturismo se necesita una estructura corporal que nunca tendrá el que quiera ganar una maratón, ni tampoco un pigmeo podrá jugar de pívot en la NBA. ¿Cómo cambia el cuerpo de estos deportistas? La solución nos la puede dar la alometría.

La alometría es el cuerpo de conocimientos que nos explican cómo cambian y cómo se relacionan algunas de las estructuras y/o funciones (ritmo cardiaco, diámetro de los vasos sanguíneos, etc.) con el tamaño de cualquier ser vivo5. Esto resulta interesante para comprender la capacidad de rendimiento del ser humano y sus posibilidades evolutivas.

Cuando el cociente de dos medidas cambia a medida que crecen, como la relación cabeza-brazo, decimos que el crecimiento es alométrico. Cuando las longitudes de ciertas partes de un organismo crecen alométricamente, el cuerpo cambia de forma a medida que crece5: como sabemos, las personas no son bebés gigantes, el crecimiento en general es alométrico. Cuando un organismo crece alométricamente algunas características o partes escalarán (seguirán leyes de escala) con la longitud del organismo, mientras que otras pueden escalar con el área superficial o con el volumen. Por ejemplo, el índice del intercambio de oxígeno podría escalar isométricamente con el área superficial de los pulmones, pero el metabolismo, el volumen sistólico, el consumo máximo o submáximo de oxígeno, las dimensiones del corazón, la ventilación alveolar, la difusión pulmonar, el volumen de aire expirado en un segundo, el volumen capilar, la síntesis de proteínas, la densidad mineral ósea, la fuerza muscular y otras muchas variables fisiológicas crecen, en condiciones normales, alométricamente con relación al tamaño del cuerpo. Todas estas relaciones responden a la necesidad del organismo de optimizar y economizar al máximo su funcionamiento cuando este realiza las funciones naturales de supervivencia.

Tradicionalmente, se asumía que la fuerza muscular se escalaba alométricamente con el peso corporal (PC) con un exponente (α) igual a 2/3 (0,666) [F = K x PC2/3; donde K es un valor que cambia con el nivel de rendimiento del deportista]6. Sin embargo, si hacemos un análisis pormenorizado de los deportes de fuerza vemos que no es exactamente así. El exponente alométrico cambia también con el tamaño del cuerpo y, por lo tanto, con el peso corporal5.

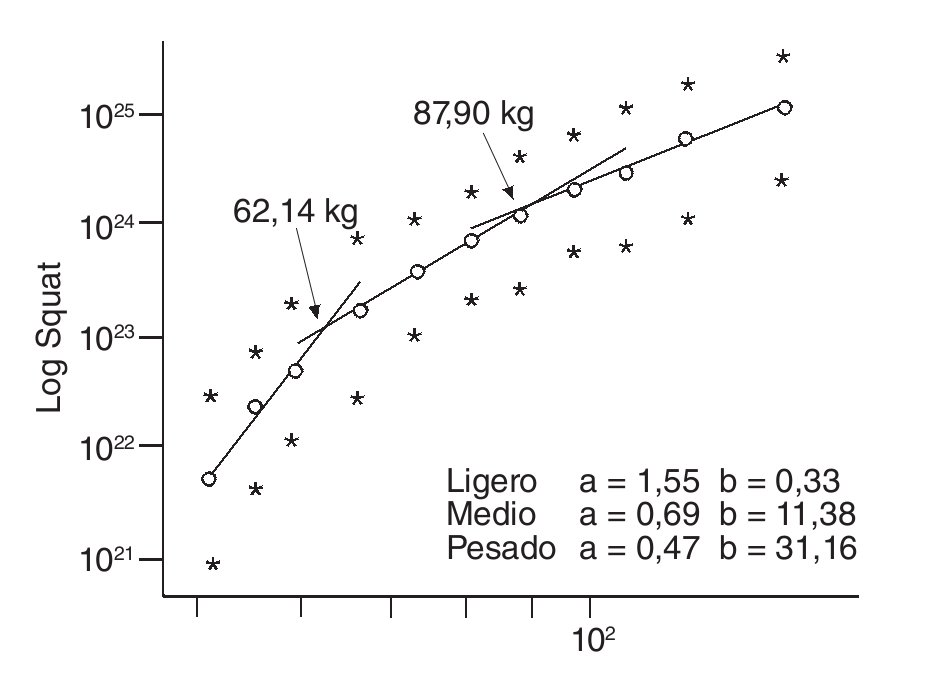
Pensemos en la modalidad de powerlifting 7. Si analizamos los rendimientos de la modalidad de sentadilla, vemos que se destacan tres zonas que engloban, por un lado las categorías de pesos en las que compiten los levantadores más ligeros (de < 52,0 kg a < 60,0 kg), otra a los medianos (de < 67,5 kg a < 90,0 kg) y otra a los pesados (de < 100 kg a > 125 kg) (fig. 1).

Fig. 1. Log-Log plot del rendimiento en sentadilla en powerlifting para cada categoría de peso con los ajustes de las rectas de regresión de cada grupo de categorías de peso corporal (ligeros, medianos y pesados). Los puntos superiores responden a los récords mundiales; los círculos blancos, a la media de los mejores; la parte inferior a la media de los levantadores con ficha de la IPF durante cinco temporadas. Tomado de García-Manso et al7.

Este resultado nos parece importante y de gran trascendencia. De hecho, encontramos de forma natural que la relación PC frente a rendimiento muestra tres PL diferentes entre sí, con cortes bien definidos, y que de ser así respondería a tres realidades deportivas significativamente diferentes. Además, demuestra que el uso tradicional de ajustes globales (polinómicos o de cualquier otro tipo) puede ocultar la dinámica interna, de carácter complejo y no lineal, de la prueba.

Los valores de α (valor de a en la fig. 1) obtenidos nos muestran que sólo los levantadores de la categoría intermedia (medianos) se ajustan a las escalas alométricas tradicionales (2/3 o 3/4). En los levantadores de pesos ligeros la pendiente es muy elevada (> 1,0), lo que indica una mayor dependencia del rendimiento con el PC, y, concretamente, con la masa muscular (MM). Lo contrario sucede en las categorías más elevadas (pesados). Todo es importante desde el punto de vista del entrenamiento y de la estrategia de competición.

Leyes de potencia y deportes individuales (atletismo)

Veamos un primer ejemplo muy característico en pruebas de carrera en atletismo8,9. En las de carreras atléticas, la distancia recorrida d y el tiempo de carrera t, siguen, sorprendentemente, una ley de escala [t(d) = cd b ].

Donde b es el exponente escala que parece ser el mismo desde la carrera de 100 metros hasta la de 10.000 metros o la maratón10. Así el exponente b medido en 1925 dio un valor de 1,141, y en 1995 fue de 1,123. Un resultado parecido se encontró para nadadores, tanto en la categoría masculina como femenina. Esto significa que existe invarianza en escala para el rendimiento humano, es decir, si cambiamos la distancia d a otro valor cd, la ecuación queda t(cd) = c bt(d) o, lo que es lo mismo, el cociente entre los tiempos para dos distancias diferentes t(cd)/t(d) = c b , depende sólo del exponente de escala b.

Pero en muchas ocasiones se encuentra más de una ley de escala, con puntos de corte, y varios exponentes de escala. En estos casos las leyes de potencia están reflejando comportamientos distintos o respuestas a fenómenos subyacentes distintos. Los ejemplos mencionados, tanto en el caso de las carreras como en la natación, se da de forma clara este hecho11.

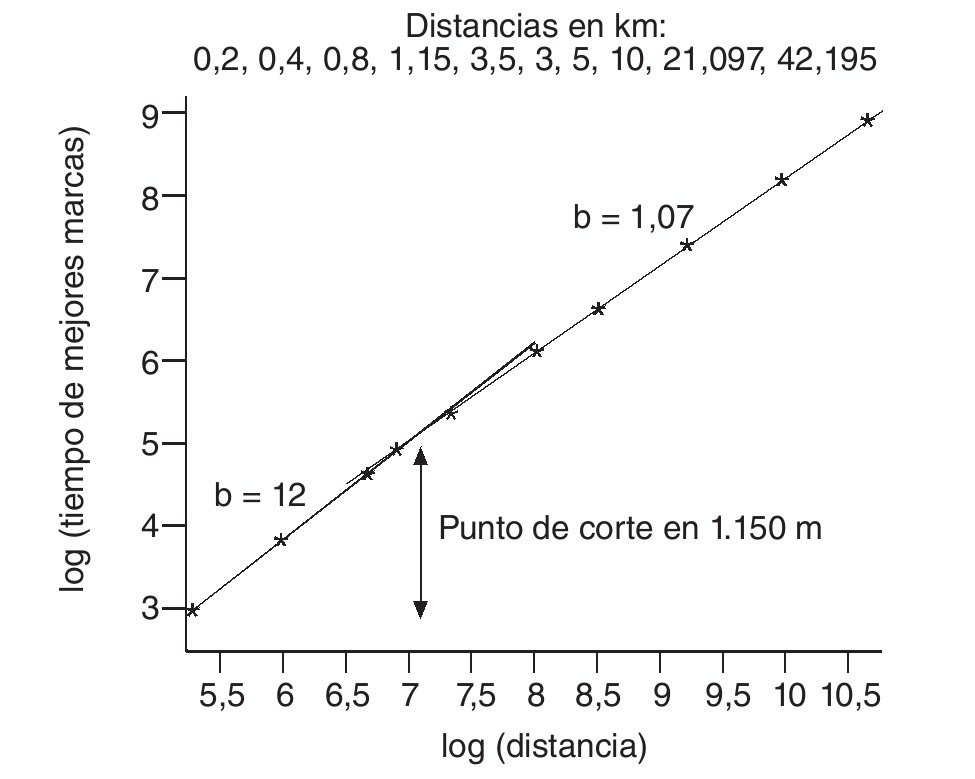
En la figura 2, se representan en el eje X los logaritmos de los valores de las distancias recorridas en cada prueba desde los 200 metros hasta la maratón y, en el eje Y, los logaritmos de los mejores tiempos obtenidos en competiciones oficiales. Aunque los datos a primera vista parecen seguir, en conjunto, una línea recta, en la curva se observa un cambio significativo en las pendientes cerca de los 1.000 metros. Este define el punto de corte de dos rectas con exponentes de escala distintos. Como señalan Savaglio y Carbone11 el comportamiento de los deportistas durante las carreras atléticas, o durante las pruebas de natación, puede considerarse un fenómeno crítico. Así, la transición entre los dos exponentes de escala define un punto cerca de los 1.150 metros que corresponde al cambio entre carreras de corta distancia, donde predomina el metabolismo anaeróbico y la fuerza, frente a las carreras de resistencia con claro componente del metabolismo aeróbico.

Fig. 2. Logaritmo del tiempo frente a la distancia en las mejores marcas de las carreras entre los 200 metros y la maratón. Se incluye el punto de corte y el valor de las pendientes de ambas rectas (gráfico realizado con datos propios, no publicados).

Si se tuvieran buenos y suficientes datos de cuáles son las mejores marcas mundiales sobre diferentes distancias de carrera (pruebas olímpicas y no olímpicas), casi con toda seguridad podríamos decir que aparecerían numerosas leyes de escala. Algunas de las más claras son las que quedan por encima o por debajo de los 1.000-1.200 metros, pero haciendo un análisis más detallado seguro que encontraríamos otras leyes de escala que agruparían distancias de características comunes (por ejemplo: de 1.000 a 5.000; de 5.000 a media maratón; de media maratón a 100 kilómetros, etc.).

El comportamiento PL también se encuentra cuando analizamos la distribución de probabilidad del fenómeno4. Este caso es especialmente importante ya que, como hemos mencionado, los sistemas complejos, por sus características, en general sólo admiten tratamiento de tipo estadístico. Pero los resultados provenientes de la estadística se basan, o sólo tienen sentido, cuando las distribuciones son de tipo normal (gaussiano) o de otro tipo donde los parámetros como valores medios, varianzas, intervalos de confianza, etc., tienen sentido. El problema principal estriba en que las colas de estas distribuciones tienden a cero con rapidez y, por tanto, no predicen con suficiente seguridad sucesos extraños, muy alejados de los valores medios, extraordinarios, avalanchas, etc1. Es decir no dan cuenta de los principales hechos de los fenómenos críticos o de SOC.

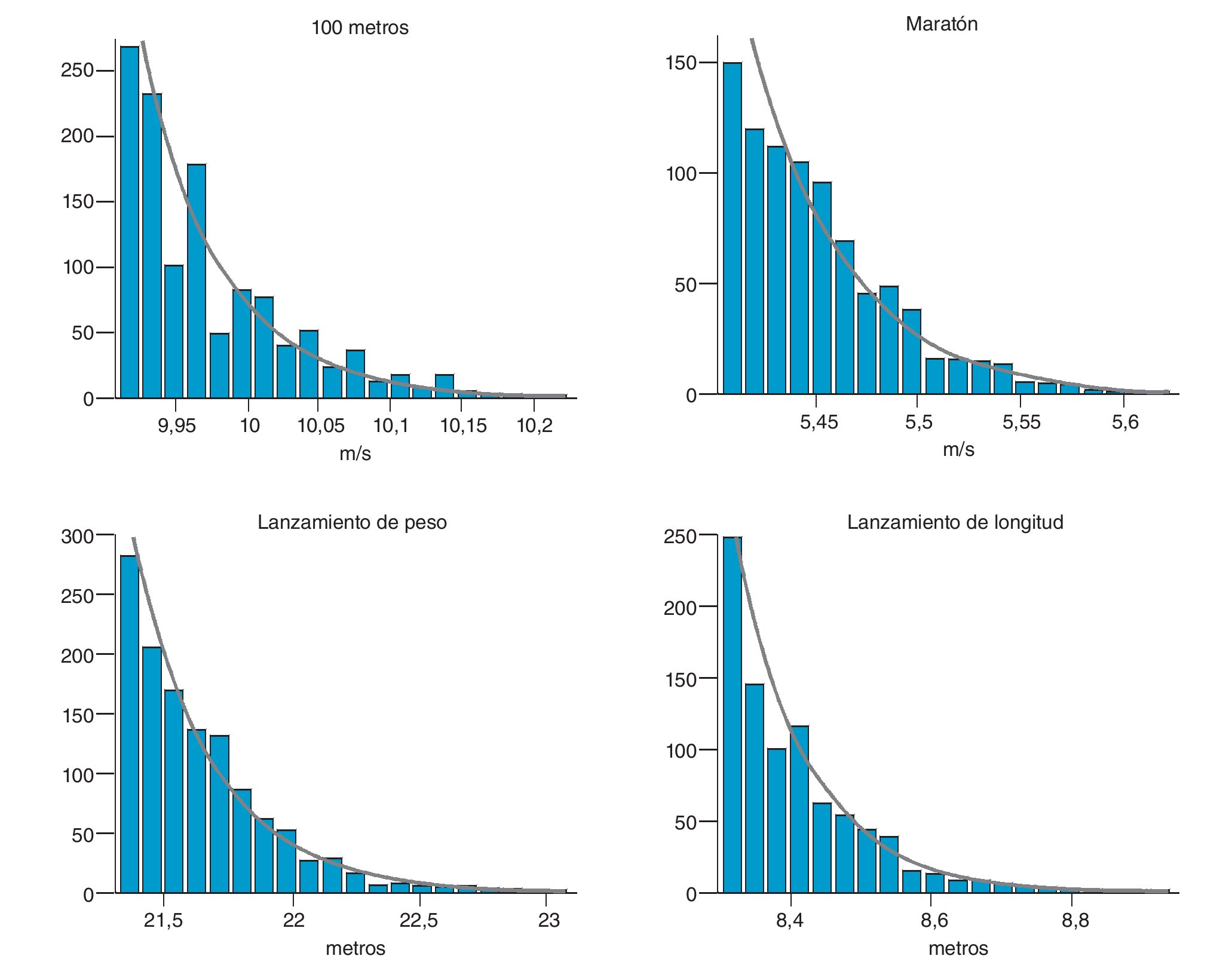
Lo que sucede a nuestro alrededor no es tan normal o gaussiano como parece y un ejemplo de ello lo tenemos en cómo se organizan las marcas obtenidas por los mejores deportistas de todos los tiempos. Para ello hemos tomado los datos de las mejores marcas por individuo de diversas competiciones atléticas como las carreras de 100 metros, la de maratón, el lanzamiento de peso o el salto de longitud, cuyos histogramas mostramos en la gráfica (fig. 3). En todos los casos hemos ajustado una PL a los valores de frecuencias del histograma, que se representa en la figura como una línea continua.

Fig. 3. Histogramas de la distribución de las marcas en las pruebas atléticas de 100 metros, maratón, lanzamiento de peso y salto de longitud. Se incluye (línea) PL (ley de potencia) de cada una de ellas.

Estos datos, desgraciadamente, no incluyen los resultados de la última olimpiada, especialmente en el caso de la carrera de 100 metros, pero este resultado refuerza el comportamiento PL de forma significativa. Nótese también que los valores de las barras del histograma, si bien siguen globalmente la ley de potencia, muestran en determinadas zonas valores significativamente más altos que en otras. Este fenómeno es relevante tal como veremos en el siguiente ejemplo.

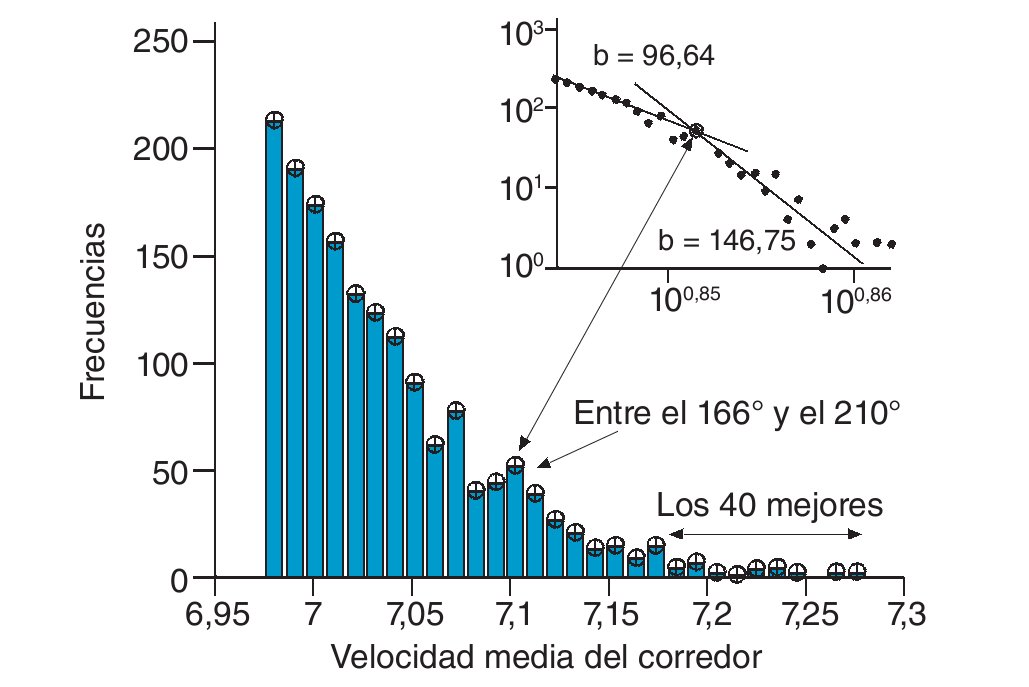
Nos centraremos en este caso, por su importancia, en la carrera de 1.500 m. La figura 4 muestra el histograma de las mejores marcas obtenidas por los 1.633 mejores corredores de la carrera de 1.500 metros en todos los tiempos. En este caso utilizamos como marca la velocidad media en m/s, es decir, el cociente entre 1.500 y el tiempo empleado en recorrerla.

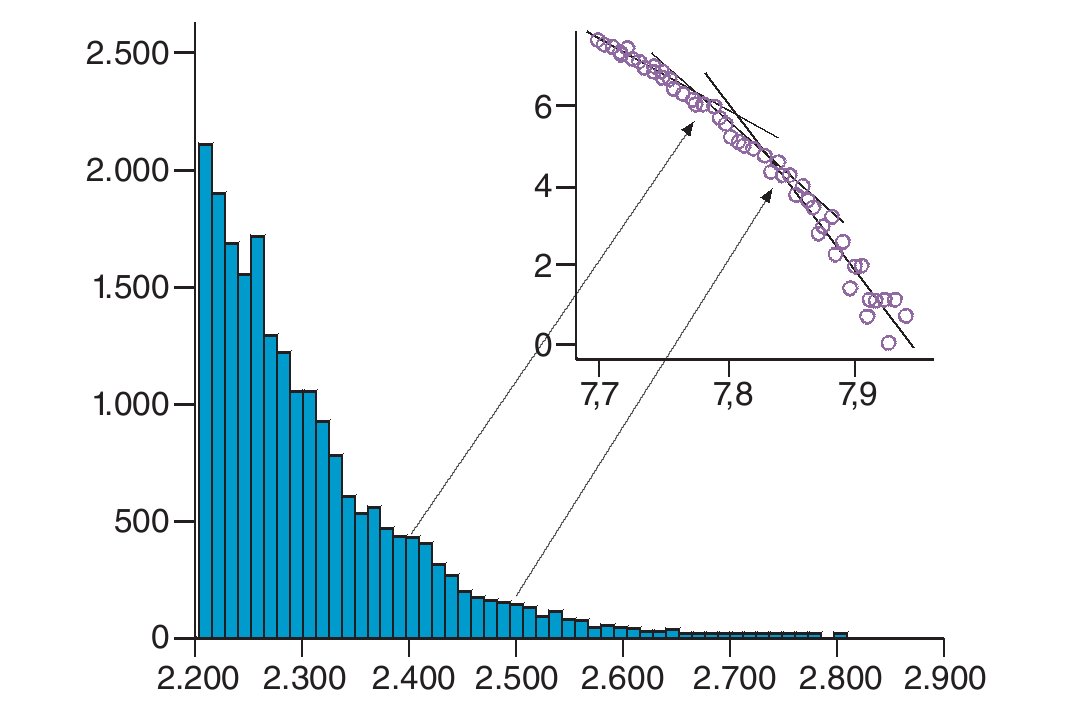
Fig. 4. Diagrama de barras de la clasificación mundial de 1.500 metros para un número de intervalos (n = 30).

La figura muestra el histograma de estos valores pero, para analizar la ley de potencia resultante, mostramos en el recuadro los logaritmos de las marcas en el eje X frente a los logaritmos de los valores de la frecuencia en el eje Y. Los valores de la frecuencia siguen dos leyes de potencia como se muestra en el recuadro, es decir dos rectas que se cortan en torno al puesto 170. Es notable, como señalamos, la aparición de intervalos más poblados que sus vecinos y de los que destacamos dos: uno en torno al valor 7,1 m/s que corresponde a los puestos entre el 166 y el 210, determinando el punto de corte de las rectas, y otro que representa a los puestos en torno al 40, que debería determinar una tercera recta y, que no se define en el recuadro, debido al pequeño número de datos. Dos puntos hemos de tener en cuenta. En primer lugar las PL definen tres zonas: antes de 170, desde 170 a 40 y mayores que 40, los tres son tipos de rendimiento competitivo. Por encima de 40 está la elite de la distancia. Si lo vemos con más detalle aún encontraremos unos, muy pocos, corredores con marcas superiores a 7,25 que representan a los mejores de la especialidad, con una diferencia importante respecto a los demás.

El segundo punto a que nos referimos tiene que ver con los intervalos más poblados. En García-Manso et al9 se señala que estos valores corresponden a las barreras, es decir, aquellos valores que un deportista tiende a alcanzar a medida que mejora su rendimiento. En otras palabras, hay unas metas fijas o marcas determinadas que funcionan, de alguna manera, como atractores y a la vez como filtros. De hecho, cuando un deportista bate un récord importante está abriendo el camino de los demás hacia una nueva barrera. De alguna manera cada deportista compite a su nivel de rendimiento, con intereses particulares y estrategias en cada competición: ganarla, hacer buena marca o, simplemente, participar en el evento para aumentar su información, hacer contactos, o darse a conocer (mecanismos de realimentación).

Leyes de potencia en los deportes de equipo

En los deportes de equipo también sucede algo parecido a lo descrito en el caso del atletismo. Quizá convenga mencionar una hipótesis algo anterior al concepto SOC, y que ya mencionamos en el trabajo anterior al hablar de los fenómenos críticos: la hipótesis de la Reina Roja 12. Esta metáfora o analogía, aplicada a sistemas ecológicos, fue formulada por Van Valen y se denomina así por el famoso libro Alicia en el país de las maravillas escrito en 1865 por Lewis Carroll. En uno de los capítulos, la Reina Roja le dice a Alicia: "Aquí, como ves hay que correr todo lo que puedas para permanecer en el mismo lugar. Si quieres ir a algún sitio, debes correr por lo menos el doble de rápido". Según esta hipótesis los seres vivos para mantener su eficacia deben estar evolucionando y mejorando sus aptitudes continuamente, lo mismo se puede aplicar a muchos otros sistemas. Debido a la presión evolutiva de un ambiente en continua transformación, los sistemas se ven en la obligación de competir en una carrera donde continuamente necesitan nuevas adaptaciones que les permitan conservar su posición relativa con respecto a los demás.

Al parecer, lo mejor es resignarse a vivir en un delicado equilibrio, en el filo de la navaja, entre el orden y el caos. Lo importante para un deportista o un equipo es mantenerse en la competición, no tanto ganar, aunque este sea el objetivo final. Ganar depende de muchos factores, algunos impredecibles, pero estar en el juego significa estar siempre intentando o buscando nuevas posibilidades, aprender, comparar, observar a otros entrenadores, comprar y vender jugadores, en definitiva seguir vivos a toda costa. Sólo para permanecer compitiendo hay que estar en perpetuo movimiento, si además se quiere ganar la liga hay que correr (evolucionar o mejorar) mucho más.

El deporte es, por tanto, un ámbito donde podemos encontrar este tipo de distribuciones. Hay algunos trabajos sobre deportes individuales como es el caso del atletismo, pero también podemos encontrar otros relacionados con los deportes de equipo, en los que también parece que se dan las PL.

Malacarne y Mendes13 consideran los mayores goleadores de campeonatos de liga de diferentes países donde el fútbol es un fenómeno de masas. Así, cuentan el número de jugadores que han marcado n goles, luego los que han marcado n-1, etc., y encuentran una ley de potencia. También Greenhough et al14 destacan la relación existente entre la distribución de los goles que se consiguen en fútbol con estadísticas de fenómenos extremos (distribuciones con colas largas).

Se han encontrado resultados parecidos al analizar en varios deportes el tiempo medio que dura un entrenador en un equipo de cierta categoría. Aidt et al15 muestran cómo el tiempo que un entrenador permanece al frente de equipos de fútbol, béisbol y fútbol americano sigue una ley de potencia con valores de los exponentes entre 2 y 3. Para ello trabajan sobre una base de datos con un total de 7.183 entrenadores. En algunos casos, los datos tienen 130 años de antigüedad. Se centran en el tiempo, en años, que cada entrenador permanece en un equipo. Analizan diferentes periodos: entre 1874-1900, 1874-1920, 1874-1966, 1874-1980 y 1874-2005, y encuentran que a medida que el sistema evoluciona la distribución se va ajustando cada vez mejor a una PL, por lo que deducen que las leyes de escala, en este contexto, son un fenómeno emergente, es decir emerge como consecuencia de la evolución del sistema; un resultado ya obtenido para otros sistemas complejos.

Leyes de potencia y deportes de dependencia cognitiva

En otro tipo de actividad deportiva, como en el ajedrez, Blasius y Toenjes16 encuentran que las aperturas más utilizadas, tanto por los jugadores aficionados como por los grandes maestros, se distribuyen de acuerdo a una PL que tiene un exponente que aumenta a medida que el juego avanza. También las clasificaciones en este deporte siguen una PL y, para verlo, primero hemos de recordar que el nivel de rendimiento del jugador de ajedrez se mide mediante un procedimiento que asigna un valor denominado ELO a cada deportista. Para comprobarlo tomamos un listado de 20.600 jugadores con un valor de ELO superior a 2.200.

La gráfica muestra el histograma de estos valores (fig. 5). Observamos en el recuadro cómo, aparentemente, hay tres líneas (tendencias) diferenciadas que presentan puntos de corte en torno a un ELO de 2.400 y 2.500. Por encima de los 2.400 hay una elite de jugadores que incluye, aproximadamente, a los 800 mejores jugadores mundiales. Si nos centramos sólo en los de valor superior a 2.500, también sigue un comportamiento lineal doble, con una "súper-élite" que abarca a los 40 primeros, cuyos valores de ELO están por encima de los 2.650, y donde se da la máxima rivalidad.

Fig. 5. Histograma que muestra cómo se distribuyen todos los jugadores de ajedrez del mundo con un ELO superior a 2.200. En el recuadro log-log de los parámetros representados en el histograma (eje X: valor del ELO; eje Y: frecuencia).

El análisis de las PL en el deporte permite localizar determinados tipos de regularidades que aparecen y, en ocasiones, permite arrojar luz en otros aspectos.

En un artículo definimos, a partir de las leyes de potencia entre distancia recorrida y velocidad y para rendimientos diferentes, un índice de rendimiento general8. Mostramos cómo este índice, que relaciona niveles de rendimiento diferentes, tiene estructura multifractal, un indicio importante de comportamiento crítico, y permite establecer criterios científicos a la hora de marcar límites de participación por nivel de rendimiento (por ejemplo, las marcas mínimas que dan derecho a participar en una competición) u organizar deportistas o equipos por niveles racionales de rendimiento.

Conclusiones

La complejidad es la característica esencial del mundo que nos rodea y de nosotros mismos, y el deporte no puede vivir de espaldas a esta realidad. Los métodos científicos tradicionales, que se fundamentan en una filosofía de tipo reduccionista, a pesar de su éxito evidente en sus campos de aplicación particulares, parecen incapaces de hacer frente a estas complejas interdependencias, de dar explicaciones o hacer predicciones convincentes. Y, aunque parece ser necesaria una nueva ciencia de la complejidad que ofrezca una metodología alternativa con la que hacer frente a esos problemas, este marco conceptual con definiciones, conceptos y principios claros, está todavía por construir. Las PL son una herramienta útil para ese concepto. En el estudio del rendimiento deportivo las PL no han sido muy utilizadas en el pasado. Su aplicación nos abre una nueva ventana desde la que observar el mundo del deporte.

Correspondencia:

J.M. García-Manso.

Campus Universitario de Tafira, s/n. Edificio de Ciencias de la Actividad Física y el Deporte. 35017 Las Palmas de Gran Canaria.

Correo electrónico: jgarcia@def.ulpgc.es

Historia del artículo:

Recibido el 31 de agosto de 2009.

Aceptado el 5 de octubre de 2009.