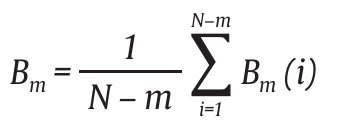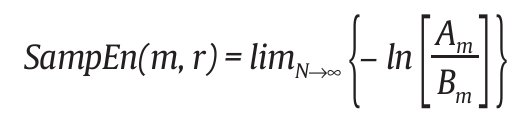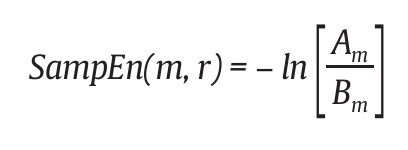Introducción

Estamos habituados a considerar dos tipos de fenómenos en la Naturaleza: los que obedecen a leyes físicas conocidas y son absolutamente previsibles, y los que son simplemente aleatorios (y por tanto impredecibles). Nos sentimos cómodos con las relaciones lineales entre magnitudes (por ejemplo: cuanto mayor es la masa de un objeto, mayor es la fuerza con que la Tierra lo atrae, es decir, su peso) y con el pensamiento de que conocidas todas las variables de un sistema podemos conocer el estado de ese sistema en cualquier instante pasado o futuro. Sin embargo, las señales fisiológicas presentan fluctuaciones complejas e irregulares que no pueden ser analizadas con técnicas estadísticas convencionales, pues proporcionan una información muy limitada de su comportamiento. La teoría del caos determinista dio lugar al desarrollo de métodos matemáticos que se han mostrado útiles en el estudio de la complejidad de señales biológicas, entre los que se incluyen el análisis de la dimensión fractal1, el exponente de Lyapunov2,3, la entropía4 y otros.

La entropía cuantifica la regularidad de un sistema, de forma que cuanto más predecible es una serie, menor es el valor de la entropía. Así, hay trabajos que muestran que con el envejecimiento se reduce la entropía, al igual que los sistemas patológicos muestran entropías menores que los sistemas sanos5.

A lo largo del tiempo han ido surgiendo varios modelos matemáticos para calcular la entropía, todos ellos con la misma finalidad: cuantificar la regularidad de una serie temporal. En 1991 Pincus introdujo la entropía aproximada (ApEn)6. Teniendo en cuenta que una serie es regular si existen patrones repetitivos en ella, la ApEn refleja la probabilidad de que patrones "similares" no sean seguidos de adicionales observaciones "similares". Una serie de tiempo que contenga muchos patrones repetitivos tendrá un valor pequeño de ApEn, mientras que a una serie menos predecible (es decir, sin patrones repetitivos, poco regular) le corresponderá un valor mayor de ApEn.

Dado que el algoritmo matemático de la ApEn compara cada patrón consigo mismo, sugiere que en una serie temporal hay más semejanza de la que en realidad existe, siendo los resultados muy dependientes de la longitud de la serie. Así surgió la entropía muestral (SampEn)7, una modificación de la ApEn, para solventar esta dependencia, con lo que los resultados son más consistentes.

Posteriormente Costa8,9 demostró que si en una serie de tiempo discreta construimos nuevas series cuyos términos son promedios de k elementos consecutivos de la serie original (siendo k el orden de la escala), y calculamos el valor de SampEn para cada una de ellas, el valor de SampEn varía cuando consideramos la estructura y organización de la serie a escalas superiores. Definió así la entropía multiescala (MSE).

Desde que se descubrió que el mecanismo implicado en el control locomotor es fundamentalmente complejo y no lineal10,11, tanto la marcha humana como el equilibrio en bipedestación han sido objeto de estudio utilizando herramientas matemáticas provenientes de las teorías del caos determinista, aunque la mayor parte de los trabajos se han centrado en el estudio del envejecimiento y de patologías que afectan a la marcha.

Así, el análisis de la dinámica no lineal ha sido utilizado para investigar las alteraciones de la marcha en la enfermedad de Huntington12, la esclerosis lateral amiotrófica13 o la enfermedad de Parkinson14, aportando información que podría ser de gran utilidad en el abordaje diagnóstico y terapéutico de estas enfermedades. Por otra parte, trabajos recientes15 muestran que el estudio de la marcha durante el envejecimiento utilizando herramientas de análisis no lineal aporta conocimientos sobre aspectos funcionales que habitualmente no se detectan con técnicas convencionales. Así, sabemos que con el envejecimiento existe una pérdida de la complejidad en el patrón de la marcha y que esta pérdida se asocia a una mayor inestabilidad y, por tanto, a un mayor riesgo de caídas16,17.

En cuanto a los métodos de análisis utilizados, los estudios más recientes coinciden en la utilización del exponente de Lyapunov y la ApEn tanto para el análisis de la variabilidad en la marcha18-21 como en el equilibrio22,23, siendo el grupo de Costa y Goldberger el único que utiliza la MSE24.

El objetivo del presente trabajo es determinar los valores de la SampEn en el análisis del equilibrio estático en sujetos sanos.

Método

Hemos estudiado un total de 12 sujetos (5 hombres y 7 mujeres), de edades comprendidas entre 18 y 25 años, a los que se realizó una exploración clínica previa para valorar la ausencia de patologías del aparato locomotor tanto en estática como en dinámica.

A todos los sujetos se les interrogó sobre sus antecedentes clínicos personales, con especial interés en aquellas actuaciones terapéuticas y patologías que pudiesen afectar a los sistemas de control del equilibrio.

La exploración realizada incluyó un examen de columna vertebral, caderas, rodillas, tobillos y pies, así como un análisis estático y dinámico de la marcha en plataforma podo-barométrica con el sistema CBS-Scan-Graf/Podocomputer®.

Tras una breve explicación acerca del procedimiento a seguir y con el sujeto en bipedestación, se procedió a registrar la proyección del centro de gravedad sobre una plataforma de fuerza Dinascan® (Instituto de Biomecánica de Valencia [IBV]) de 600 x 370 mm de área activa, utilizando el sistema de valoración del equilibrio NedSVE® (IBV).

La fuerza ejercida sobre la plataforma se reparte entre 4 captadores extensiométricos articulados que generan las correspondientes señales electrónicas en función de la carga asumida por cada uno de ellos. A partir de las ecuaciones de equilibrio estático de la placa superior de la plataforma el programa realiza el cálculo de las tres componentes de la fuerza de reacción, las coordenadas del punto de aplicación de la fuerza vertical resultante y el momento de torsión en cada instante de tiempo.

Cada sujeto se situó sobre la plataforma en bipedestación estática relajada, con los pies descalzos y haciéndolos coincidir con señales marcadas en la superficie de la plataforma para que la distancia se mantuviera constante. Los brazos quedaban extendidos y paralelos al cuerpo y esta posición se mantuvo durante la realización de todas las pruebas. En estas condiciones se efectuó una prueba tipo Romberg modificada con una duración de 60 segundos y una frecuencia de muestreo de 60 Hz; se obtuvieron 3.600 datos por cada registro. La prueba constaba de dos ensayos, uno con los ojos abiertos (ROA) manteniendo la mirada en un punto lejano, y otro con los ojos cerrados (ROC). En ambos casos el sujeto debía permanecer inmóvil. De no ser así se consideraba la prueba no válida y se repetía hasta completar los 60 segundos sin realizar movimiento alguno.

Durante cada prueba se visualizaban en tiempo real las fuerzas ejercidas sobre la plataforma en tres direcciones, así como la posición del centro de presiones. En la pantalla del ordenador se disponía de una vista superior de la plataforma en la que se representa en tiempo real la evolución del centro de presiones, las coordenadas X e Y de dicho centro y los valores en Newton de los tres componentes de la fuerza (Fz: vertical; Fx: medial-lateral; Fy: antero-posterior).

Los datos obtenidos y tabulados para el análisis fueron: el desplazamiento total de la señal, la dispersión y el desplazamiento de la señal tanto en sentido medio-lateral (eje X) como antero-posterior (eje Y), el área total de barrida y la fuerza máxima aplicada en ambos ejes.

Por otra parte, las series originales de 3.600 valores correspondientes a las coordenadas X e Y fueron utilizadas para el cálculo de la SampEn, definida como el negativo del logaritmo natural de la probabilidad condicional de que dos patrones similares de m puntos permanezcan semejantes (es decir, distancia entre ellos menor que n) si incrementamos el número de puntos a m+1.

El cálculo se realiza de la siguiente forma:

Dada una secuencia de N medidas, UN = {u1, u2, ..., uN}, sean xm (i) y xm (j) dos patrones de UN , los dos de longitud m. En xm (i) el patrón comienza en el elemento u i de la serie y en xm (j) en el elemento u j . Se define la distancia d[xm (i),x m (j)] entre dos patrones xm (i) y xm (j) como la diferencia máxima entre sus respectivos componentes, de forma que los dos patrones serán similares si d[xm (i),x m (j)] < r, siendo r el parámetro que define el criterio de similitud.

Consideramos ahora Xm como el conjunto de todos los patrones de longitud m dentro de UN (es decir, xm(1), xm(2), ..., xm (N-m+1)). Dado un patrón xm (i) se cuenta el número de patrones xm (j), donde 1 ≤ j ≤ N-m, tales que d[xm (i),x m (j)] < r. A ese número lo denominamos Bi . Así, para 1 ≤ i ≤ N-m:

La probabilidad de que dos patrones de m puntos coincidan será:

Repetimos el procedimiento para m+1 y obtenemos Am (i) y Am .

Definimos SampEn como:

N es finito, luego resulta:

La elección de m y r es fundamental para el cálculo de SampEn. Pincus6 indica que los valores idóneos son m = 1 ó m = 2 (preferiblemente m = 2) y r entre el 10 y el 25% de la desviación estándar (DE) de la serie temporal. Esto es así porque r ha de ser como mínimo mayor que el ruido que contamina la señal y además no puede tener un valor muy elevado, pues se perdería mucha información de la señal que estamos valorando. En este trabajo hemos optado por m = 2 y r = 0,25 DE.

Todos los datos se muestran como media y DE. Se realizó una prueba t de Student para muestras pareadas entre la situación de ojos abiertos y ojos cerrados, considerando significativo un valor de p menor de 0,05.

Todos los sujetos fueron informados verbalmente del contenido de la investigación y dieron su consentimiento por escrito para participar en la misma.

El protocolo de estudio fue aprobado por el Comité de Ética del Centro Andaluz de Medicina del Deporte.

Todas las pruebas fueron realizadas en el área de Fisiología del Centro Andaluz de Medicina del Deporte en Sevilla por los mismos exploradores.

Resultados

La tabla 1 muestra los datos lineales obtenidos por la plataforma de fuerza tanto con ojos abiertos como con ojos cerrados.

En la tabla 2 se recogen los valores de la SampEn en ambas situaciones (ojos abiertos y ojos cerrados).

Discusión

Este estudio aporta información que puede resultar relevante para el análisis del equilibrio humano desde el punto de vista de la dinámica de sistemas complejos.

El análisis no lineal de la marcha está extendiéndose en la literatura científica como un método útil para el estudio del envejecimiento y de algunas patologías. Sin embargo, hay aún muy pocos trabajos que empleen esta metodología en el estudio del equilibrio22,23.

Si efectuamos en nuestros sujetos un análisis convencional del equilibrio mediante datos lineales, podemos observar que todos los parámetros son mayores cuando se miden con los ojos cerrados (tabla 1), aunque esta diferencia sólo resulta significativa en lo que se refiere al área de barrida y a los valores relacionados con el eje Y. Si tenemos en cuenta que estamos estudiando a sujetos jóvenes y sin patología que afecte al equilibrio ni a la bipedestación, debemos aceptar que estos cambios ocurren sin que clínicamente sean perceptibles porque de lo contrario darían lugar a una prueba de Romberg positiva. De hecho, la interpretación clínica convencional de estos cambios podría tener que ver con cierto grado de "inestabilidad" derivado de la supresión de la información visual.

Sin embargo, la utilización de una herramienta de análisis no lineal como la SampEn podría aportar una lectura diferente. Se puede observar (tabla 2) cómo los valores de SampEn muestran un comportamiento diferente en el eje X y en el eje Y, presentando en el primer caso valores prácticamente idénticos tanto con los ojos cerrados como abiertos. En el eje Y los valores de SampEn son menores que en el eje X en ambas situaciones, pero existe un descenso significativo al registrar con los ojos cerrados.

Según los valores de SampEn (tabla 2) debemos concluir que el comportamiento del centro de gravedad en el eje Y es más predecible que en el eje X a pesar de que el análisis lineal (tabla 1) muestra un mayor desplazamiento del centro de masas en sentido antero-posterior (eje Y) al cerrar los ojos, sin apenas cambios en sentido medio-lateral (eje X). En este eje el valor de entropía nos indica que el sistema conserva un alto grado de complejidad que se mantiene inmutable con independencia de que los ojos estén abiertos o cerrados.

En definitiva, el empleo de la SampEn podría aportar nuevas perspectivas en el análisis del equilibrio y podría ser de gran utilidad cuando se valoren situaciones patológicas del aparato locomotor.

Correspondencia:

J. Naranjo Orellana.

Centro Andaluz de Medicina del Deporte. Glorieta Beatriz Manchón, s/n. 41092 Sevilla. España.

Correo electrónico: jose.naranjo@juntadeandalucia.es

Historia del artículo:

Recibido el 1 de septiembre de 2008

Aceptado el 7 de octubre de 2008